Data science

Data Science (data wetenschappen) is eigenlijk een wat vreemde term. Iedere tak van wetenschap draait immers om data. Van psychologie tot economie en van geschiedkunde tot natuurkunde, er worden data verzameld om daar vervolgens conclusies uit te trekken die bijdragen aan kennis. Data Science is het vakgebied dat zich bezighoudt met het proces om vanuit data naar inzicht te komen. Met de enorme datagroei van de afgelopen decennia en parallel hieraan de sterk toegenomen computer rekenkracht, speelt Data Science een steeds belangrijkere rol. Want dat data waarde hebben is algemeen bekend, maar hoe zorg je dat je door de bomen het bos nog steeds ziet of zelfs… steeds beter ziet?

Bij het AMLC zien we ons in de witwasbestrijding ook regelmatig met die vraag geconfronteerd. Binnen de Data&Analyse groep van het AMLC wordt gewerkt aan de AMLC-browser en het analyse framework daarachter, dat allerlei databronnen als een netwerk kan visualiseren. Netwerkvisualisaties zijn handig voor de rechercheur en analist. In plaats van te kijken naar bijvoorbeeld een lange lijst verdachte transacties met vele kolommen, kan de samenhang tussen rekeningen in één oogopslag duidelijk worden door een netwerk representatie van dezelfde data: rekeningen als knooppunten en transacties daartussen als connecties.

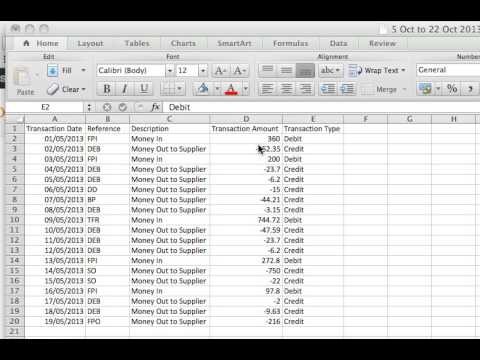
Figuur 1. Transactie data in tabelvorm (boven) en in netwerkvorm (onder).

Niet alleen voor de gebruiker is een netwerkweergave vaak veel duidelijker, ook computers zijn in staat complexere vragen veel sneller te beantwoorden op data in netwerkvorm dan in tabelvorm. Vooral wanneer het gaat om indirecte relaties zoals: geef mij alle ‘routes’ over maximaal 4 verschillende rekeningen die rekening A verbindt met rekening B.

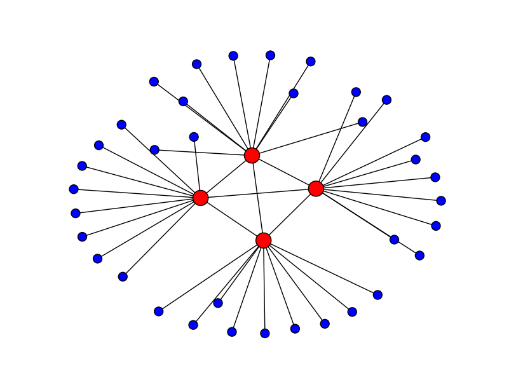
In de wiskunde is er ook speciale aandacht voor netwerken (wiskundigen noemen het grafen). Netwerken bestaan uit knooppunten en connecties die kunnen dienen als model voor allerlei verschillende entiteiten, zoals bankrekeningen en transacties in het vorige voorbeeld, maar ook mensen en onderlinge vriendschappen, telefoonnummers en onderlinge telefoongesprekken, of stations en spoorlijnen, kortom van alles. Data scientists maken veel gebruik van concepten uit de grafentheorie omdat die algemeen gelden voor netwerken. Een heel simpel voorbeeld van zo’n concept is de ‘degree’ van een node: het aantal connecties van een node. Een node met een hoge degree speelt bijna automatisch een belangrijke rol in een netwerk, omdat het verbonden is met zoveel andere nodes. In bijna ieder efficiënt georganiseerd netwerk vind je een aantal hoge degree nodes dat onderling ook nog eens goed verbonden is. In onze spoorwegen kun je denken aan Utrecht, Rotterdam, Amsterdam, Zwolle en Den Bosch. Dit zijn hubs waarvandaan je heel veel kanten op kunt zowel lokaal met sprinters als verder weg met intercity’s. Onderling gaan er tussen deze stations iedere 10 minuten treinen. Dit fenomeen van onderling sterk verbonden hubs wordt ook wel het ‘rich club’ effect genoemd (nodes rijk aan verbindingen vormen een hechte club).

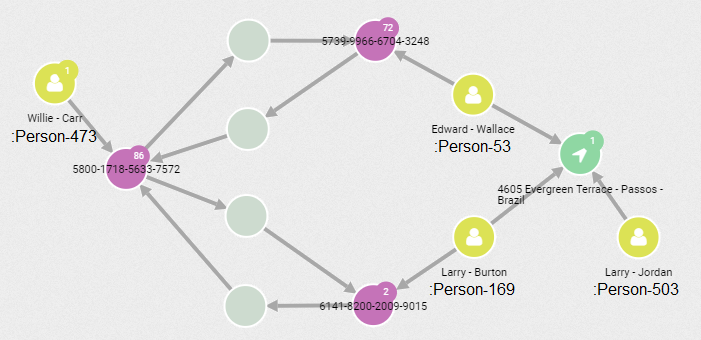
Bij het AMLC hebben we deze ‘rich club’ analyse uitgevoerd op de metadata[1] van de Panama papers en Paradise papers[2] om te onderzoeken of dit effect ook aanwezig is in netwerken van personen en/of bedrijven genoemd in deze Leaks. Tijdens een data challenge met de J5-landen[3] hebben we met behulp van dit type analyse mogelijke facilitators (key players) in kaart gebracht die minimaal banden hadden met 2 van de J5-landen.

Figuur 2. Rich club nodes (rood).

Door middel van machine learning (zelflerende algoritmes) methodes kunnen we nog een stap verder gaan en zelfs entiteiten met elkaar in verband brengen die geen directe / indirecte relaties met elkaar hebben. Door de rol van een node in zijn eigen netwerk te typeren (degree, verhouding inkomende / uitgaande connecties, verhouding connecties met hubs / non hubs etc..), krijgen we een reeks objectieve maten die samen een soort netwerk vingerafdruk vormen van een node. Op basis hiervan kan een algoritme op zoek gaan naar soortgelijke nodes in een heel ander (deel van een) netwerk. Op deze manier kunnen entiteiten door een algoritme gegroepeerd worden op basis van de netwerkeigenschappen. De groepen die het algoritme vindt, kunnen een bevestiging zijn van wat we verwachten: adressen van een trustkantoor waarop 100+ bedrijven staan ingeschreven zullen wel in één groep terecht komen vanwege hun bijzondere netwerkvorm. Maar wellicht zien we ook een groep ontstaan van entiteiten die we niet meteen aan elkaar hadden gelinkt en die misschien wel op een nieuwe constructie of fenomeen duiden. Hier hopen we een volgende keer over te kunnen berichten.

[1] Metadata zijn de eigenschappen van de documenten. Een voorbeeld hiervan is de verzenddatum of onderwerp van een email.

[2] Grote hoeveelheid gelekte documenten die inzicht geven in verhullende financiële constructies

[3] Joint chiefs of global tax enforcement: Verenigde Staten, Canada, Australië, Verenigd Koninkrijk, Nederland